Age of Information for Multi-agent systems

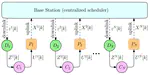
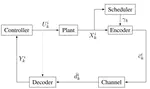
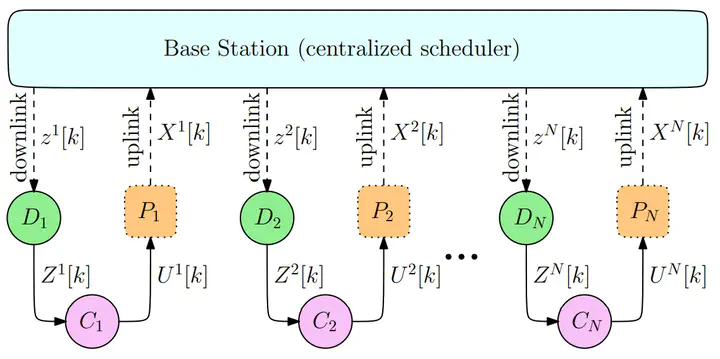
In this project, we consider a discrete-time multi-agent system involving N cost-coupled networked rational agents solving a consensus problem and a central Base Station (BS), scheduling agent communications over a network. Due to a hard bandwidth constraint on the number of transmissions through the network, at most Rd < N agents can concurrently access their state information through the network. Under standard assumptions on the information structure of the agents and the BS, we first show that the control actions of the agents are free of any dual effect, allowing for separation between estimation and control problems at each agent. Next, we propose a weighted age of information (WAoI) metric for the scheduling problem of the BS, where the weights depend on the estimation error of the agents. The BS aims to find the optimum scheduling policy that minimizes the WAoI, subject to the hard bandwidth constraint. Since this problem is NPhard, we first relax the hard constraint to a soft updaterate constraint, and then compute an optimal policy for the relaxed problem by reformulating it into a Markov Decision Process (MDP). This then inspires a sub-optimal policy for the bandwidth constrained problem, which is shown to approach the optimal policy as N → ∞. Next, we solve the consensus problem using the mean-field game framework wherein we first design decentralized control policies for a limiting case of the N–agent system (as N → ∞). By explicitly constructing the mean-field system, we prove the existence and uniqueness of the mean-field equilibrium. Consequently, we show that the obtained equilibrium policies constitute an ǫ–Nash equilibrium for the finite agent system. Finally, we validate the performance of both the scheduling and the control policies through numerical simulations.