Linear Quadratic Mean-Field Games with Communication Constraints
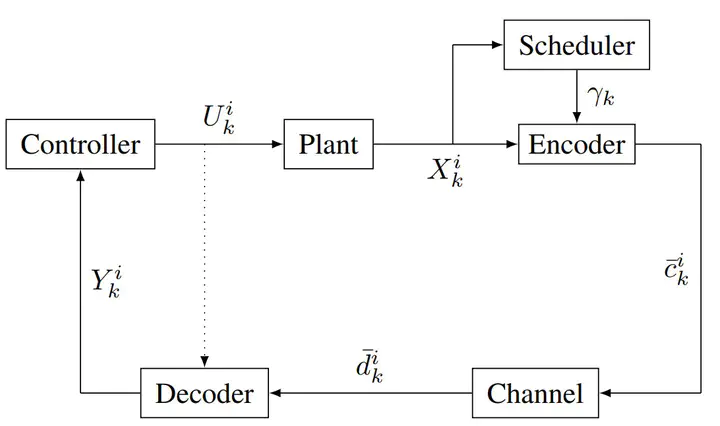 Image credit: Unsplash
Image credit: Unsplash
Abstract
— In this paper, we study a large population game with heterogeneous dynamics and cost functions solving a consensus problem. Moreover, the agents have communication constraints which appear as (1) an Additive-White Gaussian Noise (AWGN) channel, and (2) asynchronous data transmission via a fixed scheduling policy. Since the complexity of solving the game increases with the number of agents, we use the MeanField Game paradigm to solve it. Under standard assumptions on the information structure of the agents, we prove that the control of the agent in the MFG setting is free of the dual effect. This allows us to obtain an equilibrium control policy for the generic agent, which is a function of only the local observation of the agent. Furthermore, the equilibrium mean-field trajectory is shown to follow linear dynamics, hence making it computable. We show that in the finite population game, the equilibrium control policy prescribed by the MFG analysis constitutes an approximate Nash equilibrium. The paper is concluded with simulations demonstrating the performance of the equilibrium control policy
#Supplementary notes can be added here, including code, math, and images.