Multi-Agent RL in multiple populations

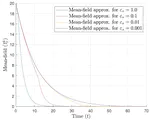
Scalability of reinforcement learning algorithms to multi-agent systems is a significant bottleneck to their practical use. In this project, we approach multi-agent reinforcement learning from a mean-field game perspective, where the number of agents tends to infinity. Our analysis focuses on the setting where agents are assumed to be partitioned into finitely many populations connected by a network of known structure. The functional forms of the agents’ costs and dynamics are assumed to be the same within populations, but differ between populations. We first characterize the equilibrium of the mean-field game which further prescribes an approximate Nash equilibrium for the finite population game. Our main focus is on the design of a learning algorithm, based on zero-order stochastic optimization, for computing mean-field equilibria. The algorithm exploits the affine structure of both the equilibrium controller and equilibrium mean-field trajectory by decomposing the learning task into first learning the linear terms and then learning the affine terms. We present a convergence proof and a finite-sample bound quantifying the estimation error as a function of the number of samples